La somme de Riemann offre une définition opérationnelle de l’intégrale. Elle s’appuie sur une partition de l’intervalle et sur des points choisis dans chaque sous-intervalle pour construire une somme de rectangles qui converge vers l’intégrale lorsque le pas des subdivisions tend vers zéro. Cette approche est essentielle en CPGE pour comprendre l’intégration et elle sert d’outil discret dans les méthodes numériques d’approximation.
Somme de Riemann : définition et notations essentielles
Vous introduisez d’abord l’intervalle [a, b] et la partition P: a = x_0 < x_1 < ... < x_n = b. Chaque sous-intervalle [x_{i-1}, x_i] possède une largeur Δx_i = x_i - x_{i-1}.
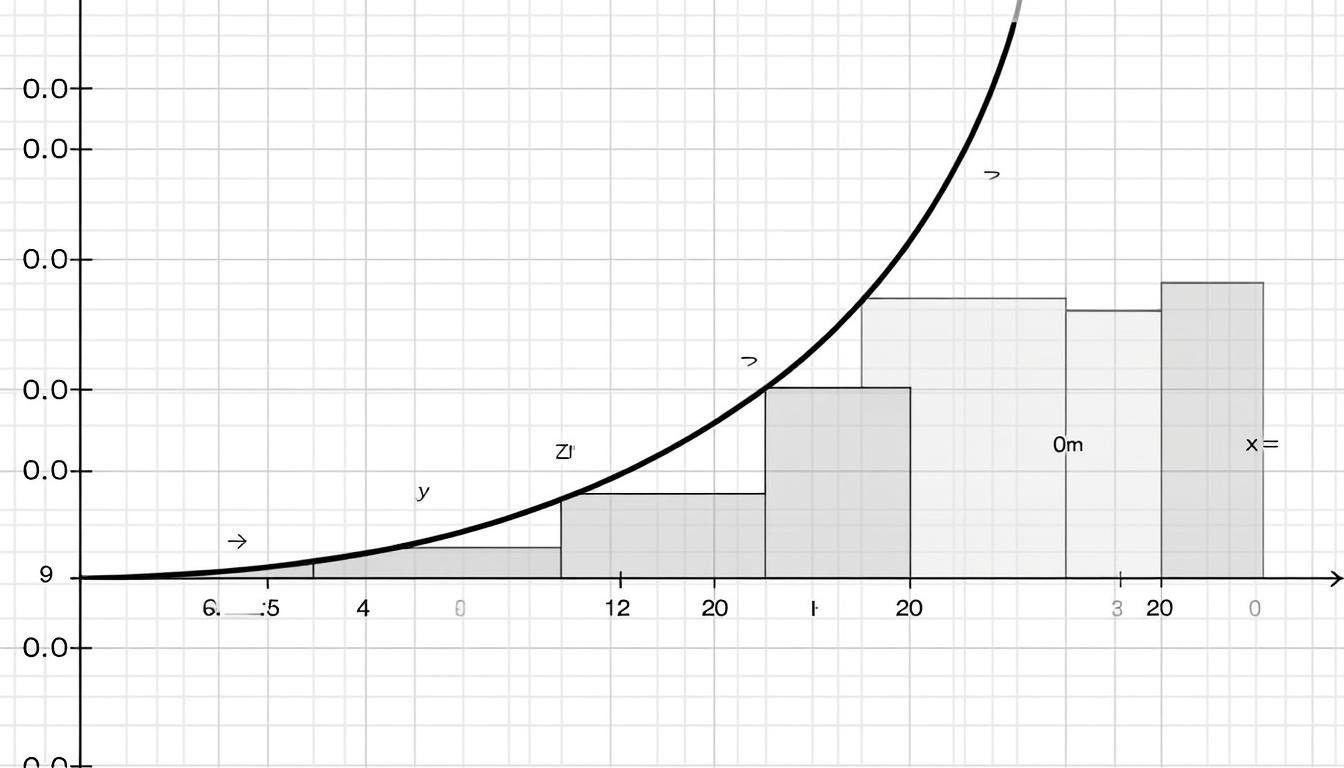
- Partition d’un intervalle : défini par les points x_i et les longueurs Δx_i; elle délimite les rectangles qui vont approximer l’aire sous la courbe.
- Somme de Riemann : S(f; P, {ξ_i}) = ∑_{i=1}^n f(ξ_i) (x_i − x_{i-1}), avec ξ_i ∈ [x_{i-1}, x_i].
- Convergence et intégrabilité : si f est bornée sur [a,b], alors la norme ||P|| = max_i Δx_i tend vers zéro et toutes les sommes convergent vers une même valeur I = ∫_a^b f(x) dx.
- Intégrale définie : I = ∫_a^b f(x) dx est la limite de S(f; P, {ξ_i}) lorsque ||P|| → 0, pour les partitions qui rendent l’erreur arbitrairement petite.
- Pas de la subdivision et encadrement : le pas maximal ||P|| mesure la finesse de la subdivision; des encadrements utilisent les sommes inférieures et supérieures pour évaluer l’intégrale.
La différence entre les sommes inférieures et supérieures illustre l’intégrabilité. On définit S_inf(f, P) = ∑ m_i Δx_i et S_sup(f, P) = ∑ M_i Δx_i, où m_i et M_i sont respectivement les infimum et supremum de f sur [x_{i-1}, x_i]. L’intégrale est atteinte lorsque la borne inférieure et la borne supérieure coïncident sous toutes les partitions appropriées.
Procédure en étapes pour une intégrale par somme de Riemann
- Choisir l’intervalle [a, b] et la fonction f définie et bornée sur cet intervalle.
- Construire une partition P de [a, b], puis calculer ||P||.
- Sélectionner les points ξ_i dans chaque sous-intervalle et former S(f; P, {ξ_i}).
- Faire tendre ||P|| vers zéro et vérifier la convergence vers ∫_a^b f(x) dx.
- Utiliser des sommes inférieures et supérieures si nécessaire pour encadrer l’intégrale lors d’estimations rapides.
Exemple central entièrement résolu
Considérons f(x) = x^2 sur l’intervalle [0,1]. On choisit une partition régulière avec x_i = i/n et ξ_i = x_{i-1}.
- Expression de la somme de Riemann : S_n = ∑_{i=1}^n f(ξ_i) Δx_i = ∑_{i=1}^n ((i-1)/n)^2 · (1/n).
- Calcul du regroupement : S_n = (1/n^3) ∑_{i=1}^n (i-1)^2 = (1/n^3) ∑_{j=0}^{n-1} j^2.
- Utilisation de la formule ∑_{j=0}^{m} j^2 = m(m+1)(2m+1)/6 : on obtient S_n = ((n-1)n(2n-1)) / (6 n^3).
- Limite lorsque n → ∞ : S_n → 1/3, et donc ∫_0^1 x^2 dx = 1/3.
- Conclusion : pour ce f et cette partition, la somme de Riemann converge exactement vers l’intégrale, et la vitesse de convergence dépend du choix de la partition et des points ξ_i.
Précisions secondaires et variantes
La théorie distingue plusieurs cas et variantes utiles en préparation des concours.
- Cas limites et continuité : une fonction bornée sur [a,b] est intégrable au sens de Riemann si et seulement si la limite des sommes de Riemann, en raffermissant les partitions, existe et est indépendante du choix des points ξ_i (à conditions raisonnables). En pratique, des fonctions avec un petit nombre de discontinuités restent intégrables.
- Cas particuliers utiles : pour des fonctions en escalier ou continues par morceaux, l’intégrale se décompose en somme d’intégrales sur chaque morceau, ce qui simplifie les calculs et les estimations.
- Erreurs fréquentes : confondre limite de la somme et valeur immédiate; négliger le rôle du pas de subdivision; oublier que la convergence peut dépendre de la régularité de f; croire qu’une somme de Riemann approximative suffit sans contrôle d’erreur.
- Encadrement et méthodes numériques : les sommes de Riemann sous-tendent les méthodes numériques classiques (trapèzes, rectangles, Simpson) pour l’approximation d’intégrales lorsque les formes fermées sont indisponibles.
- Lien avec l’intégrale définie : la règle fondamentale affirme que l’intégrale est la limite des sommes lorsque ||P|| → 0; la vitesse de convergence dépend de la régularité de f et du choix de la partition.
Pour approfondir, l’encadrement par les sommes inférieures et supérieures constitue une base robuste pour les estimations d’intégrales. Lorsque n devient grand et que f est monotone ou continue, les écarts S_sup − S_inf diminuent et l’intégrale est isolée avec précision.
Applications pratiques et mise en oeuvre en CPGE
La somme de Riemann sert de passerelle entre le raisonnement analytique et l’approximation numérique. Sa mise en œuvre suit une démarche claire qui permet de traiter des intégrales sans forme fermée.
- Étapes méthodiques : déterminer f et l’intervalle; vérifier l’intégrabilité; choisir une partition adaptée; calculer S; faire tendre ||P|| vers zéro; estimer l’erreur.
- Encadrement rapide : utilisez S_inf et S_sup pour obtenir des bornes utiles lorsque l’intégrale exacte est inconnue.
- Cas concrets : pour f monotone ou continue, les erreurs se réduisent comme O(1/n) dans des partitions régulières simples; des partitions adaptatives peuvent améliorer la vitesse de convergence.
- Liens avec les notions voisines : la méthode éclaire l’intégration numérique et clarifie le passage de la somme à l’intégrale; elle prépare aux développements sur les suites et les limites.
Exercice type avec corrigé bref
Énoncé : Sur l’intervalle [0,1], prenez f(x) = x et une partition régulière en n sous-intervalles avec ξ_i = x_{i-1}. Écrivez S_n et montrez que lim_{n→∞} S_n = ∫_0^1 x dx = 1/2.
- Corrigé bref :
- Avec x_i = i/n et ξ_i = x_{i-1}, Δx_i = 1/n et f(ξ_i) = (i-1)/n.
- Donc S_n = ∑_{i=1}^n (i-1)/n · 1/n = (1/n^2) ∑_{i=1}^n (i-1) = (1/n^2) · n(n-1)/2 = (n-1)/(2n).
- La limite est 1/2 lorsque n → ∞, ce qui vérifie l’égalité ∫_0^1 x dx = 1/2. En outre, pour ξ_i = x_i, on obtient S'_n = ∑ i/n · 1/n = (1/n^2) ∑ i = (n+1)/(2n) → 1/2 également.
À retenir :
- Définition de la somme de Riemann est S(f; P, {ξ_i}) = ∑ f(ξ_i)(x_i - x_{i-1}).
- Partition d’un intervalle et pas de subdivision déterminent l’approximation; le pas idéal tend vers zéro.
- L’intégrale définie est la limite des sommes lorsque ||P|| → 0.
- Les sommes inférieures et supérieures fournissent des encadrements utiles et éclairent l’intégrabilité.
- Pour les fonctions continues ou monotones sur [a,b], l’erreur d’approximation diminue avec le raffinement de P.
- En CPGE, maîtriser le passage de la somme à l’intégrale prépare aux méthodes numériques et à l’analyse rigoureuse.
- L’exemple x^2 sur [0,1] illustre le mécanisme de convergence et l’obtention de la valeur exacte 1/3.
- Utiliser les sommes pour encadrer des intégrales sans forme fermée est une compétence clé des exercices d’annales.
