La loi de Cauchy, aussi appelée loi de Lorentz, est une distribution continue qui ne possède ni espérance ni variance. Sa densité est lorentzienne et dépend de deux paramètres: la localisation x0 et l’échelle a > 0. Elle sert notamment à modéliser des raies spectrales en spectroscopie et à illustrer les limites des lois classiques (généralisation: distribution extrême). Cette loi est stable avec index 1 et peut apparaître comme le quotient de deux normales indépendantes. En 2025, elle demeure un cadre fondamental pour comprendre les limites des moments et des moyennes dans les concours.
Notions clés autour de la loi de Cauchy (densité, localisation, échelle)
Dénsitée (fonction qui associe à chaque valeur x la probabilité par unité d’intervalle) se note f et se décrit par:
f(x) = a / (π [a^2 + (x - x0)^2]), avec x0 la localisation et a l’échelle (> 0).
La version centrée et réduite est obtenue avec x0 = 0 et a = 1, soit f(x) = 1 / (π (1 + x^2)).
Caractéristiques essentielles :
- La loi est symétrique par rapport à x0.
- Le paramètre a détermine la dispersion (demi-largeur à mi-hauteur).
- Le quotient X/Y de deux variables normales standards indépendantes suit une Loi de Cauchy.
- La loi est stable avec indice α = 1; le moment d’ordre un n’existe pas.
Pour la forme standard, la densité est f(x) = 1/(π(1+x^2)), et la fonction de répartition est F(x) = (1/π) arctan(x) + 1/2.
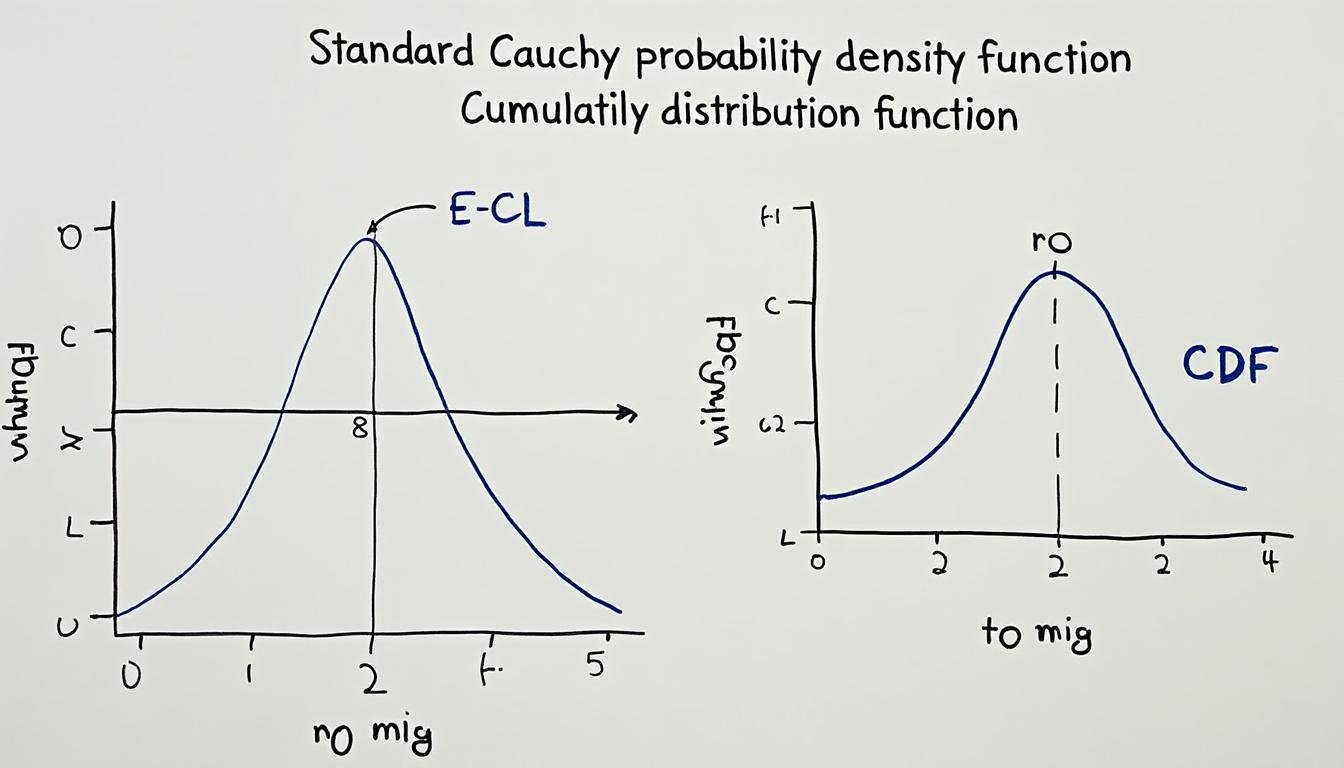
Exemple central entièrement résolu : densité, CDF et absence d’Espérance
Objectif : démontrer les formules clés pour X ~ Cauchy(x0, a) et vérifier l’absence d’espérance.
- Densité standard : pour X ~ Cauchy(0,1), f(x) = 1/(π(1+x^2)).
- Densité et CDF généralisées : pour X ~ Cauchy(x0, a),
f(x) = a/(π [a^2 + (x - x0)^2]),
F(x) = (1/π) arctan((x - x0)/a) + 1/2. - : l’intégrale E(X) = ∫ x f(x) dx diverge, car
∫_{-∞}^{+∞} x/(a^2 + (x - x0)^2) dx ne converge pas. : si X et Y sont indépendantes et suivies de N(0,1), alors
Z = X/Y suit une Loi de Cauchy standard : Z ~ Cauchy(0,1).
Justification condensée : le couple (X,Y) suit une densité normale bidimensionnelle indépendante. En passant en coordonnées polaires (R, Θ), Θ est uniforme sur (-π, π], et Z = X/Y = cot Θ. La densité de Z est alors 1/(π(1+z^2)).
Propriétés remarquables et liens avec d'autres lois
Propriétés remarquables :
- Absence d’espérance et d’écart-type : E(X) et Var(X) n’existent pas.
- Quantiles : q(p) = x0 + a tan(π(p - 1/2)). Par exemple, q(0.75) = x0 + a.
- Caractéristique : la fonction caractéristique est φ(t) = exp(-a|t|) exp(i x0 t).
- Stabilité : toute combinaison linéaire de variables Cauchy donne une autre Cauchy (indice 1).
- Relation avec les extrêmes : la distribution est une des distributions « Sans Moyenne », source de ProbaParadoxe dans les démonstrations théoriques.
Liens importants :
- Le quotient X/Y de normales standard est une Loi de Cauchy.
- La loi de Cauchy est un cas spécial de loi stable avec paramètre de stabilité égal à 1.
- La densité est singulière (aucune dérivée nécessaire pour le raisonnement élémentaire).
Applications et repères pratiques :
- Distribution extrême et phénomènes avec queues lourdes nécessitent une modélisation sans moyenne.
- Connaître la forme exacte permet d’éviter les approximations qui échouent dans les essais de concours.
| Propriété | Formule/Description | Remarque |
|---|---|---|
| Densité | f(x) = a/(π[a^2+(x-x0)^2]) | Pour x ∈ ℝ |
| CDF | F(x) = (1/π) arctan((x-x0)/a) + 1/2 | Limites 0 et 1 |
| Espérance | n’existe pas | ∞ divergence de ∫ xf(x) dx |
| Caractéristique | φ(t) = exp(-a|t|) exp(i x0 t) | Liens avec stabilité |
Applications et approfondissements
La loi de Cauchy normalise les idées autour des propriétés extrêmes et des limites. Elle illustre le fait qu’une distribution peut avoir des queues lourdes sans être « grossièrement dominée par des moments ». Dans les concours, elle sert d’outil pédagogique pour souligner les hypothèses nécessaires à l’application de la loi des grands nombres et du théorème central limite.
Exercice type et corrigé bref
Exercice : Soit X ~ Cauchy(2, 3). Calculer P(2 ≤ X ≤ 5) et donner le quantile q(0.9).
- Utiliser la fonction de répartition F(x) = (1/π) arctan((x-2)/3) + 1/2.
- Calculer P(2 ≤ X ≤ 5) = F(5) − F(2).
- Calculer le quantile 0.9 : q(0.9) = 2 + 3 tan(π(0.9−0.5)) = 2 + 3 tan(0.4π).
Correction :
F(5) = (1/π) arctan((5−2)/3) + 1/2 = (1/π) arctan(1) + 1/2 = 1/4 + 1/2 = 3/4.
F(2) = (1/π) arctan(0) + 1/2 = 1/2.
P(2 ≤ X ≤ 5) = 3/4 − 1/2 = 1/4. Quantile 0.9 : q(0.9) ≈ 11.23.
À retenir
La loi de Cauchy est une distribution continue sans espérance ni variance. Sa densité f(x) = a/(π[a^2+(x−x0)^2]) est lorentzienne et symétrique autour x0, avec a l’échelle. La CDF est F(x) = (1/π) arctan((x−x0)/a) + 1/2. Le quotient de deux normales standard suit une Cauchy. L’absence d’espérance s’explique par la divergence de l’intégrale ∫ xf(x) dx. Dans les exercices, les quantiles se calculent par x0 + a tan(π(p−1/2)).
Pour les révisions, rapprocher ces propriétés des notions de Mathématiques Stat et ProbaParadoxe aide à reconnaître rapidement les cas où la moyenne échoue. Les démonstrations autour des limites des moments renforcent l’esprit critique nécessaire aux épreuves écrites et orales. Dans la pratique, le plus utile reste la connaissance explicite des formules et leur manipulation sans approximation.
