Loi de Student : densité t, degrés de liberté, table et applications

La loi de Student s'applique lorsque l'on souhaite estimer la moyenne d'une population à partir d'un échantillon, avec une variance inconnue. Elle décrit la densité t (distribution t de Student) et s'utilise pour construire des intervalles de confiance et pour tester des hypothèses sur une moyenne. Le nombre de degrés de liberté, noté ν, est généralement ν = n − 1 pour un échantillon de taille n. Le tableau de la Table de Student permet de lire les valeurs critiques t à partir de ν et du risque d'erreur α. Cette approche est centrale en statistique inférentielle pour les tests sur moyenne et les comparaisons de moyennes lorsque la variance n’est pas connue. Ces notions trouvent leur cadre dans les épreuves typiques des concours et dans l’analyse d’échantillons réels.

Notions clés : définition et formules essentielles autour de la loi de Student

La densité t de Student, notée Tν, dépend du nombre de degrés de liberté ν et s'écrit :

f_T(t) = Γ((ν+1)/2) / (√(νπ) Γ(ν/2)) · (1 + t²/ν)^{-(ν+1)/2},

où Γ est la fonction gamma. Cette densité est symétrique autour de 0 et ressemble à la loi normale quand ν est grand. On écrit Tν ~ Student(ν) pour signifier que T suit une loi de Student avec ν degrés de liberté. Dans les méthodes d’inférence, l’indicateur clé est la statistique de Student :

T = (X̄ − μ0) / (S / √n),

avec X̄ la moyenne de l’échantillon, μ0 la moyenne hypothétique, S l’écart-type mnéque de l’échantillon et ν = n − 1.

Pour un test ou un intervalle autour de μ, il faut lire sur le tableau Table de Student les valeurs critiques tα/2,ν correspondant au risque d’erreur α et au nombre de degrés de liberté. En pratique, on compare |T| à tα/2,ν pour décider du rejet ou non de H0. Le cas échéant, l’intervalle de confiance à 1 − α est donné par :

X̄ ± tα/2,ν · (S / √n).

Au concours, il faut savoir lire le tableau pour ν donnés et α fixes, puis appliquer les formules ci-dessus sur vos données. L’intervalle et le test utilisent la même statistique et les mêmes hypothèses : distribution normale des erreurs et variance inconnue.

Exemple central entièrement résolu (application directe)

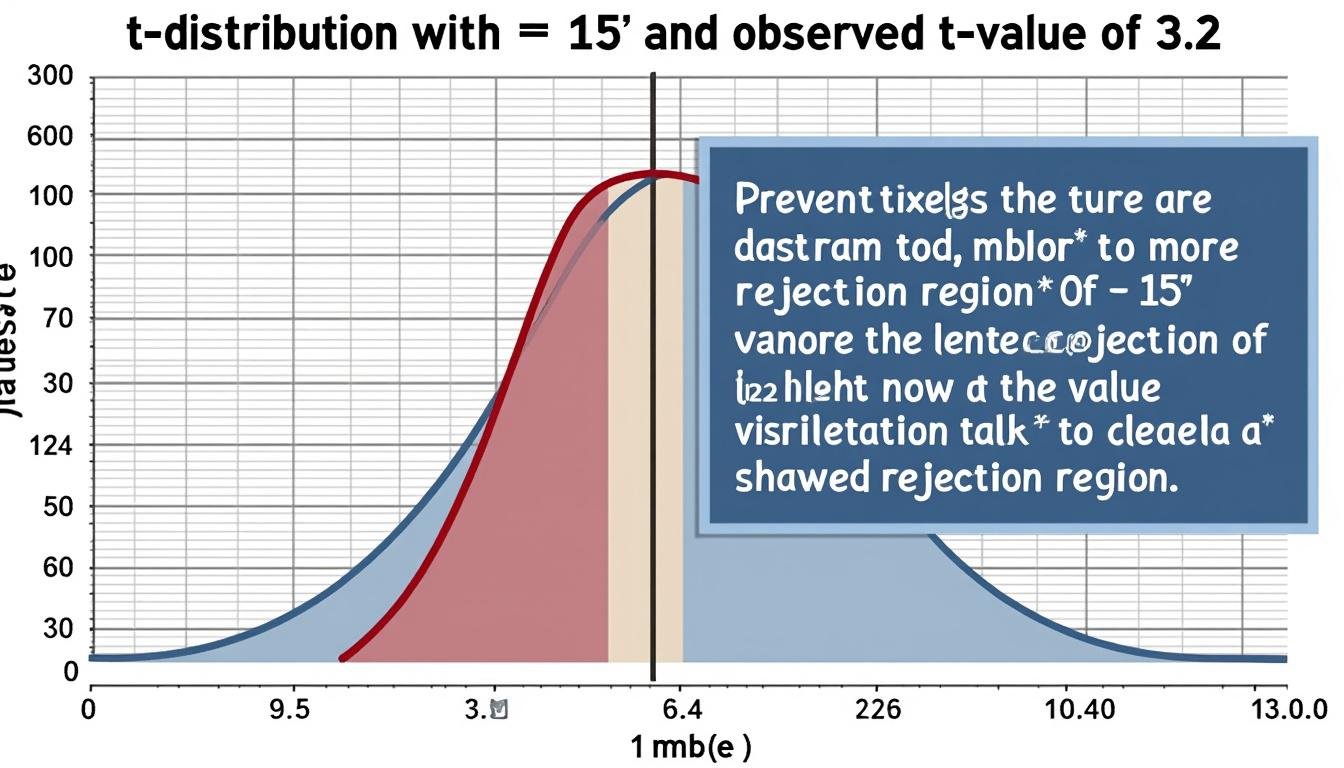
Échantillon de n = 16, X̄ = 5.8, S = 1.0, hypothèse μ0 = 5, niveau α = 0.05 (deux côtés). On calcule :

1. Définir ν = n − 1 = 15.
2. Calculer la statistique de Student :
3. T = (5.8 − 5) / (1.0 / √16) = 0.8 / 0.25 = 3.2.
4. Lire la valeur critique sur le Tableau de Student pour ν = 15 et α = 0.05. On obtient tα/2,ν = t0.025,15 ≈ 2.131.
5. Décision : |T| = 3.2 > 2.131 → rejeter H0 au niveau 5 %.
6. Intervalle de confiance à 95 % pour μ :
7. X̄ ± tα/2,ν · (S / √n) = 5.8 ± 2.131 · (1 / 4) ≈ 5.8 ± 0.5325 → [5.2675, 6.3325].

Interprétation : l’intervalle contient μ = μ0 ? Non, il ne le contient pas pour μ0 = 5, et le test indique une différence statistiquement significative à 5 %. Le p-value est compris entre 0.005 et 0.010 pour ν = 15 et T = 3.2 (valeurs tabulées correspondantes). Le cadre est l’application du Test de Student et de la Densité de probabilité t pour une Variance inconnue.

Exercice type bref avec corrigé

Exercice : On dispose d'un échantillon de taille n = 12, X̄ = 4.2, S = 0.8, H0 : μ = 4, α = 0.05.

Corrigé rapide :

1. ν = n − 1 = 11.
2. T = (4.2 − 4) / (0.8 / √12) = 0.2 / (0.8 / 3.464) = 0.2 / 0.2309 ≈ 0.866.
3. Valeur critique pour ν = 11 et α = 0.05 (deux côtés) ≈ t0.025,11 ≈ 2.201.
4. Décision : |T| = 0.866 < 2.201 → ne pas rejeter H0.
5. Intervalle de confiance à 95 % pour μ :
6. 4 ± 2.201 · (0.8 / √12) ≈ 4 ± 0.509 → [3.491, 4.509].

Conclusion : à partir de cet échantillon, aucune preuve statistiquement significative ne permet d’affirmer que μ diffère de 4 au niveau 5 %. Cet exercice illustre l’usage du Test de Student et de l’intervalle de confiance quand la variance est inconnue.

Précisions secondaires : limites, variantes et erreurs courantes

Cas limites et liens avec d'autres notions :

• Lorsque ν → ∞, Tν converge vers la loi normale standard N(0,1); la densité de probabilité t s’aligne sur la densité normale.
• Le test et l’intervalle reposent sur une variance inconnue et nécessitent l’utilisation de la statistique de Student plutôt que du z (loi normale).
• Pour la même α et ν, les valeurs critiques augmentent quand ν diminue; plus de degrés de liberté rapprochent la t-distribution de la normale, permettant des intervalles plus étroits.
• En pratique sur concours, les valeurs critiques t se lisent directement dans le Table de Student et servent à décider des rejets et à construire les intervalles.
• La comparaison de moyennes entre échantillons dépend de la même approche lorsque la variance est inconnue et qu’elle peut être supposée homogène.

Erreurs fréquentes :

• Confondre l’intervalle centré sur X̄ avec une moyenne hypothétique sans ajustement pour ν et α.
• Utiliser la densité t sans mentionner ν ni préciser s’il s’agit d’un test unilatéral ou bilatéral.
• Ignorer que la variance inconnue impose l’emploi d’une distribution t et non normale dans l’interprétation du CI.

Pour approfondir, consulter les ressources :

• Loi de Student (Wikipedia)
• Distribution de t de Student (Wikipedia)
• T-distribution sur StatisticShowTo
• The Student t-Distribution (LibreTexts)
• Le statut étudiant en prépa — enjeux et perspectives

À retenir

• Test de Student et distribution t permettent d’estimer μ lorsque la variance est inconnue et que l’échantillon est limité.
• ν = n − 1 est le nombre de degrés de liberté qui détermine la forme de la densité t et les valeurs critiques.
• Pour un test bilatéral au niveau α, comparez |T| à tα/2,ν et utilisez X̄ ± tα/2,ν (S/√n) pour l’intervalle de confiance.
• La densité t se réduit vers la normale quand ν est grand; les résultats convergent alors vers les méthodes classiques avec variance connue.
• Les valeurs critiques t sont tabulées dans la Table de Student et s’utilisent pour les décisions en concours.
• Lorsque l’écart-type est estimé, le test et l’intervalle reposent sur la statistique T et la densité t plutôt que sur la loi normale.
• Connaître le cadre « Test de Student », « Densité de probabilité t », « Degrés de liberté », « Table de Student » et « Intervalle de confiance » est indispensable pour les travaux d’échantillon et les comparaisons de moyennes.
• Entraînez-vous sur des exemples avec n varié et ν croissant pour automatiser la reconnaissance des situations courantes en concours.

Liens utiles et ressources complémentaires

• Le statut étudiant en prépa — enjeux et perspectives
• Loi de Student
• Distribution de t de Student
• T-distribution – Statistic ShowTo
• The Student t-Distribution (LibreTexts)